Dividindo por  e ordenando o polinómio do lado esquerdo pelas potências decrescente de
e ordenando o polinómio do lado esquerdo pelas potências decrescente de 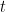 , obtemos – se escolhermos
, obtemos – se escolhermos 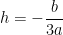
Se exprimirmos a variável 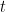 na soma de duas outras
na soma de duas outras
a equação  transforma-se em
transforma-se em
Somos assim conduzidos ao problema de achar dois números 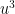 e
e  dos quais se sabe a soma
dos quais se sabe a soma 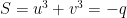 e o produto
e o produto 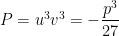 . Como é bem sabido esses números são as duas soluções
. Como é bem sabido esses números são as duas soluções  e
e  da equação auxiliar do 2.º grau:
da equação auxiliar do 2.º grau:
De facto
e
Resolvendo-a determinamos
Nesta notação o discriminante  é igual a
é igual a
Consideremos, sem perda de generalidade, 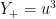 e
e  . Introduzindo
. Introduzindo  e
e 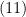 em
em 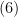 , obtemos a solução
, obtemos a solução ![t_{1}=\sqrt[3]{Y_{+}}+\sqrt[3]{Y_{-}} t_{1}=\sqrt[3]{Y_{+}}+\sqrt[3]{Y_{-}}](http://s0.wp.com/latex.php?latex=t_%7B1%7D%3D%5Csqrt%5B3%5D%7BY_%7B%2B%7D%7D%2B%5Csqrt%5B3%5D%7BY_%7B-%7D%7D&bg=ffffff&fg=000000&s=0) :
:
ou seja
e uma solução da equação inicial
Conhecida a solução  , podemos determinar as duas restantes
, podemos determinar as duas restantes 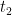 e
e 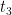 decompondo o polinómio do primeiro membro de
decompondo o polinómio do primeiro membro de  num produto de factores lineares:
num produto de factores lineares:
ou
Os dois polinómios são equivantes se tiverem iguais coeficientes homólogos:
Novamente temos de determinar dois números 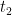 e
e 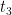 dos quais se conhece a soma (
dos quais se conhece a soma ( ) e o produto (
) e o produto ( ). Para esse fim formamos a equação do 2.º grau:
). Para esse fim formamos a equação do 2.º grau:
que resolvida dá as soluções
As três soluções da equação em  são então:
são então:
No caso do discriminante ser negativo, 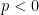 , convertemos os complexos conjugados
, convertemos os complexos conjugados  e
e 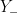 à forma trigonométrica
à forma trigonométrica

Os módulos são iguais:
e os argumentos são simétricos, sendo o de  :
:
As três raízes cúbicas de  e
e 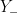 são (
são ( )
)
Obtemos, respectivamente, para 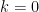 ,
, 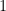 e
e 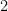 as três soluções da equação
as três soluções da equação  :
:
e as da equação original  :
:
Exemplos
1. Determine as soluções da equação
Pondo
a equação transforma-se em
uma vez que os seus coeficientes são
e
As suas soluções são 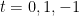 , a que correspondem as da equação na forma canónica
, a que correspondem as da equação na forma canónica 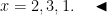
2. Resolva
Como era de esperar a substituição é
e os coeficientes da equação em 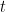
são simplesmente os da equação inicial divididos por 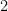 :
:
e
O discriminante é negativo
Assim, como 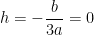 :
:
Tentando diminuir os erros de cálculo, reparemos que o inteiro 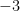 é uma solução. Se recalcularmos as outras duas, obtemos as soluções exactas:
é uma solução. Se recalcularmos as outras duas, obtemos as soluções exactas:
e
3. Resolva a equação
Fazendo a substituição
obtém-se a equação
em que
e
Uma solução da equação em 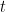 é dada pela fórmula resolvente
é dada pela fórmula resolvente
a que corresponde a solução da equação em  :
:
As restantes soluções da equação em 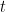 são
são
e, portanto, as da equação em  são
são
Adenda: a equação seguinte aparece nesta questão de Rajesh K Singh no MSE
—
Nenhum comentário:
Postar um comentário