Você Sabia ?

Achei Interessante esse vídeo, já vi faz um tempo, mas lembrei dele ontem quando estava vendo uma reportagem sobre as redes sociais então resolvi postar aqui.. é bem legal, olhem, vale a pena.

  

Os Polinômios ( Saiba um pouco da história)

A grande maioria das pessoas que estão em processo de aprendizagem em matemática sempre buscam aplicações imediatas para os conteúdos. Não que esse deva ser um caminho único a ser seguido, pelo contrário, a compreensão de seu valor abstrato, perpassante do território da realidade, é indubitavelmente importante. Faço aqui um comparativo entre duas matemáticas, que por mais que sejam admiráveis, tem seus campos estudados por pesquisadores diferentes. É sabido que os matemáticos reconhecem a existência dessas duas matemáticas, porém dificilmente dominam as duas simultânea e profundamente.

Falo da matemática utilitária e da matemática abstrata. Enquanto a primeira se relaciona com as questões diárias, os problemas, as demandas, ou seja, questões atuais que requerem soluções imediatas, a outra se refere ao pensamento abstrato, o conhecimento pensado e criado no campo da imaginação, do mundo teórico. É bom frisar que a matemática utilitária não se relaciona apenas com questões praticas, mas também a teorias abstratas que reflitam ao pensamento moderno decorrente da realidade vigente.

O filósofo grego Platão diferenciava a matemática utilitária, importante para comerciantes e artesãos, da matemática abstrata, destinada a elite. Um representante dessa elite foi Alexandre da Macedônia, também conhecido por Alexandre o Grande, que teve como seu preceptor Aristóteles. Mas foi no século III a.C. que surgiu o matemático Arquimedes de Siracusa, esse talvez tenha sido o primeiro a desenvolver com competência as duas matemáticas da qual estamos nos referindo. 

Outros Aplicativos

Oii, olha eu denovo, falando sobre os aplicativos sobre matematica para Android: achei outros legais ontem, e sao gratis:

   Se chama Basic Operations, ele te mostra as contas e vc tem que responder todas corretamente, tem 3 fases de cada operacao matemnatica, e a ultima fase tem tempo.

  

 

                                                                                                                                          Bjs, Luna.

 

 

Aplicativos

Oii gente.. eu , como tenho mania de tecnologia, baixo vários aplicativos no meu Android.. Hoje na sala de aula, o professor fez uma atividade diferente com a gente nos ipad's, ele pediu que baixasse um aplicativo de matemática nos ipad's do colégio pra nossa sala fazer essa atividade... No final de tudo achei super interessante, o aplicativo é muito bom !! trabalha nosso raciocínio rápido e nosso conhecimento das operações matemáticas. Cheguei em casa e tentei baixar esse aplicativo, que chama "Rei da Matemática":

O aplicativo é muito bom, só que é pago... a parte triste da historia kk.. Mas vale a pena!!! tem outros aplicativos bons também: 

Esse chama "Math Training" .. vou pesquisar mais e boto aqui! 

                                                                                                                                 Bjs, Luna.

O Blog

Nossos editores :

Rose, Gabrielle, Lucas e Luna.

Professor responsável: Luiz Carlos

Colégio Batista Brasileiro

Siga nosso Twitter: @aquelamatematic

Em breve faremos videos para postar no Youtube 

Polinômios e Álgebra

    O cálculo de equações polinomiais e algumas equações algébricas era um dos grandes desafios da chamada álgebra clássica. Os primeiros registros e conclusões sobre as relações existentes nas equações de primeiro e segundo graus foram apresentados por Al-Khowarizmi , foi ele quem apresentou em suas obras o significado da palavra álgebra, que é “trocar os membros” no termo de uma equação.

Quase meio milênio depois foram aparecendo inúmeros matemáticos como Girolamo Cardano, Niccolo Tartaglia e Ludovico Ferrari que iniciaram estudos sobre equações de terceiro e quarto graus. Alguns matemáticos se destacaram por grandes demonstrações que ajudaram e são de extrema importancia até hoje como Nuls Henrik Abel (Norueguês), Carl Friedrich Gauss (Alemão) e o Francês Evarist Galois. Cada passo realizado  para o aperfeiçoamento  de equações polinomiais de grau n, com n pertencendo ao conjunto dos números naturais, foi e é sempre de muita utilidade. Para encontrarmos o valor numérico de um polinômio p(x), sempre foram utilizados métodos de operações usuais (adição, subtração, multiplicação e divisão) conhecendo ou não uma das raízes da equação polinomial. Na soma e subtração dos polinômios basta adicionarmos  ou subtrairmos os termos de mesmo grau. Na divisão de polinômios podemos observar vários métodos . 

Exercícios Polinômios

1°) Adição de Polinômios 

a) (2x²-9x+2)+(3x²+7x-1) 
b) (5x²+5x-8)+(-2x²+3x-2) 
c) (3x-6y+4)+(4x+2y-2) 
d) (5x²-7x+2)+(2x²+7x-1) 
e) (4x+3y+1)+(6x-2y-9)
f) (2x³+5x²+4x)+(2x³-3x²+x) 
g) (5x²-2ax+a²)+(-3x²+2ax-a²)
h) (y²+3y-5)+(-3y+7-5y²) 
i) (x²-5x+3)+(-4x²-2x) 
j) (9x²-4x-3)+(3x²-10)


2°) Subtração de Polinômios 

a) (5x²-4x+7)-(3x²+7x-1)
b) (6x²-6x+9)-(3x²+8x-2) 
c) (7x-4y+2)-(2x-2y+5) 
d) (4x-y-1)-(9x+y+3) 
e) (-2a²-3ª+6)-(-4a²-5ª+6) 
f) (4x³-6x²+3x)-(7x³-6x²+8x) 
g) (x²-5x+3)-(4x²+6) 
h) (x²+2xy+y²)-(y²+x²+2xy)  
i) (7ab+4c-3a)-(5c+4a-10)


3°) Multiplicação de Polinômios


a) 3(x+y) 
b) 7(x-2y) 
c) 2x(x+y) 
d) 4x (a+b)
e) 2x(x²-2x+5) 
f) (x+5).(x+2) 
g) (3x+2).(2x+1) 
h) (x+7).(x-4) 
i) (3x+4).(2x-1) 
j) (x-4y).(x-y)
k) (5x-2).(2x-1)


4°) Divisão de Polinômios 

a) ( x³ + 2x² + x ) : (+x) =
b) (x² + x³ + x⁴) : (+x²) =
c) (3x⁴ - 6x³ + 10x²) : (-2x²) =
d) (x⁷ + x⁵ + x³) : (-x²)
e) ( 7x³ + 27x² - 3x + 4 ) : ( x + 4)
f) (2x³ + 3x² - x – 2) : ( 2x – 3)
g) ( x³ - 6x² + 7x + 4) : (x² - 2x – 1)
h) (3x³ - 13x² + 37x – 50 ) : ( x² -2x + 5)
i) ( 10x³ - 31x² + 26x – 3) : ( 5x² - 8x + 1)
j) ( 4x⁴ - 14x³ + 15x² -17x + 5 ) : (x² - 3x + 1)




  

Ajuda

Esta precisando de ajuda em algum assunto matemático??? Nó ajudamos! deixe seu comentário aqui em baixo.

Onde usamos os Polinômios ??

As vezes nós nos perguntamos onde os assuntos matemáticos entram no nosso dia a dia... Aqui vao só alguns exemplos:

Polinômios no Parque de diversões 

Desde que os polinômios são usados para descrever curvas de diversos tipos, as pessoas costumam utilizá-los para visualizar curvas. Construtores de montanhas-russas podem usar polinômios para descrever as curvas de seus trilhos, e também combinações de funções polinomiais às vezes são usadas em estudos de economia para fazer análises de custo.

Polinômios na modelagem e física

Polinômios podem também ser usados para modelar diferentes situações, como no mercado de ações, a fim de prever como os preços podem variar ao longo do tempo, ou como o aumento e queda dos preços de determinado bem irá afetar sua venda. Os polinômios, ainda, podem ser usados na física para descrever a trajetória de um projétil, e os polinômios integrais (soma de diversos polinômios) podem ser usados para expressar conceitos como energia, inércia e diferença voltaica, por exemplo.

Polinômios na Indústria

Para pessoas que trabalham em indústrias que lidam com fenômenos físicos ou modelando situações futuras, os polinômios são muito úteis, e incluem a todos, desde engenheiros a executivos. Para o resto de nós, eles estão menos aparentes, mas provavelmente ainda o usamos para predizer como a mudança de um ponto em nossas vidas pode influenciar outro, mesmo sem percebermos.

Extra: Polígonos

Classificação dos polígonos

Lados/Nomes

3: Triângulo------ 3 lados
4: Quadrilátero-- 4 lados 
5: Pentágono---- 5 lados 
6: Hexágono----- 6 lados 
7: Heptágono---- 7 lados 
8: Octógono----- 8 lados 
9: Eneágono---- 9 lados 
10: Decágono-- 10 lados 
11: Hendecágono ou Undecágono -- 11 lados 
12: Dodecágono ------------------------ 12 lados 


Polígonos convexos e não convexos

Se todos os segmentos de reta com extremos no interior de um poligono tiverem todos os pontos situados no interior do poligono ele será convexo.

se um segmento de reta tem extremos dentro do polígono mas nem todos os pontos do segmento estão dentro dele, ele sera não convexo.

Calcular Diagonais de um polígono

Diagonal de um polígono é o segmento de reta que liga um vértice ao outro, passando pelo interior da figura. O número de diagonais de um polígono depende do número de lados (n) e pode ser calculado pela expressão:





Classificação dos triângulos

Polinômios Opostos ou Simétricos

Foram dados os seguintes Polinômios:

A =   x²  -  7x  +  12 e

B = - x²  +  7x  -  12

O que ocorrerá ao efetuarmos a adição entre eles?

x²  -  7x  +  12

-x²  +  7x  -  12

0x²  +  0x  +  0

- Obtivemos um Polinômio Nulo, pois todos os seus coeficientes são iguais a Zero.

- Polinômios como estes, que adicionados resultam no Polinômio Nulo, são chamados de Polinômios Opostos ou Simétricos. 

- Notamos que, para obtermos o oposto de um certo Polinômio não - nulo, basta que troquemos os sinais de todos ou seus termos.

Ex.: O oposto de:

4x  +  3y  -  2xy é →

-4x  -  3y  +  2xy

Redução de Termos Semelhantes

Assim como fizemos no caso dos monômios, também podemos fazer a redução de polinômios através da adição algébrica dos seus termos semelhantes.

No exemplo abaixo realizamos a soma algébrica do primeiro com o terceiro termo, e do segundo com o quarto termo, reduzindo um polinômio de quatro termos a um outro de apenas dois.

Polinômios reduzidos de dois termos também são denominados binômios. Polinômios reduzidos de três termos, também são denominados trinômios.

Veja abaixo alguns exemplos de redução de polinômios através da soma ou subtração de termos semelhantes:

 

Grau do Polinômio

O grau de um polinômio reduzido, não nulo, é o grau do seu termo de maior grau.

O polinômio -5x⁴ + 14x⁵y² - 7x³y² é do grau 7, pois o seu termo de maior grau é o segundo, que é do grau 7.

O polinômio 4a²b³ + 5a⁵ é do grau 5, pois ambos os termos do polinômio são deste grau. 

Monômios, Binômios e Trinômios.

• Monômio, quando há apenas um termo; 

Denominamos monômio ou termo algébrico quaisquer expressões algébricas representadas por um número, por uma incógnita, ou pelo produto de números e incógnitas, assim 2, x, 2x e -3xy² são exemplos de termos algébricos ou monômios.

No monômio -3xy² o número -3 representa o seu coeficiente numérico e a sua parte literal é representada porxy².

Por convenção omitimos o coeficiente numérico quando ele é igual a 1, escrevemos x em vez de escrevermos 1x, por exemplo, ou então -x no lugar de -1x.

Temos um monômio nulo quando o coeficiente numérico é igual a 0, assim o termo algébrico 0x² é igual a 0.

Acima utilizamos o número 2 como um exemplo de monômio. De fato todo número real é um monômio, só que sem a parte literal.

• Binômio, quando há dois termos; 

Pelos produtos notáveis, sabemos que (a+b)² = a² + 2ab + b².
    Se quisermos calcular (a + b)³, podemos escrever:

(a + b)³ = a³ + 3a²b + 3ab² + b³

    Se quisermos calcular 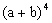, podemos adotar o mesmo procedimento:

(a + b)⁴ = (a + b)³ (a+b) = (a³ + 3a²b + 3ab² + b³) (a+b)

= a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

    De modo análogo, podemos calcular as quintas e sextas potências e, de modo geral, obter o desenvolvimento da potência 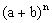 a partir da anterior, ou seja, de .
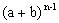    Porém quando o valor de n é grande, este processo gradativo de cálculo é muito trabalhoso.
    Existe um método para desenvolver a enésima potência de um binômio, conhecido como binômio de Newton (Isaac Newton, matemático e físico inglês, 1642 - 1727). Para esse método é necessário saber o que são coeficientes binomiais, algumas de suas propriedades e o triângulo de Pascal. 

• Trinômio, quando há três termos                                                                                              Os trinômios do tipo x² + Sx + P podem ser escritos pela forma fatorada (x + a) * (x + b), pois temos:
  
  (x + a) * (x + b) = x² + xb + xa + ab = x² + x(a + b) +ab
  
  Observe que o termo ligado à incógnita x é originado pela soma de a com b e o termo constante é resultado da multiplicação de a por b. Portanto, todas as multiplicações envolvendo (x + a) * (x + b) são representadas pela expressão x² + Sx + P.
  
  No trinômio x² + 2x – 24, temos que a forma fatorada é dada pela expressão (x + 6) * (x – 4), pois:
  
  Soma = 6 – 4 = 2
  Produto = 6 * (–4) = –24 

Divisão de Polinômios

Em toda divisão temos dividendo, divisor, quociente e resto, como estamos falando de divisão de polinômio por polinômio, teremos:

Para o dividendo um polinômio G(x)
Para o divisor um polinômio D(x)
Para o quociente um polinômio Q(x)Para o resto (podendo ser zero) um polinômio R(x)



Prova real:    

Tem algumas observações a serem feitas, como:

? ao final da divisão o resto sempre tem que ser menor que o divisor: R(x) < D(x).

? quando o resto for igual a zero, a divisão é considerada exata, ou seja, o dividendo é divisível pelo divisor. R(x) = 0.

Observe a divisão de polinômio por polinômio abaixo, vamos partir de um exemplo, cada passo tomado no desenvolvimento da divisão será explicado.

Dada a divisão
(12x³ + 9 – 4x) : (x + 2x² + 3)

Antes de começar a operação temos que fazer algumas verificações:
? se todos os polinômios estão em ordem conforme as potências de x.

No caso da nossa divisão devemos ordenar, ficando assim:
(12x³ - 4x + 9) : (2x² + x + 3) 

? observar se no polinômio G(x) não está faltando algum termo, se estiver devemos completar.

No polinômio 12x³ - 4x + 9 está faltando o termo x², completando ficará assim:
12x³ + 0x² - 4x + 9

Agora podemos iniciar a divisão:



? G(x) tem 3 termos e D(x) tem 3 termos. Pegamos o 1º termo de G(x) e dividimos pelo 1º termo de D(x):12x³ : 2x² = 6x, o resultado multiplicará o polinômio 2x² + x + 3 e o resultado dessa multiplicaçãosubtrairemos pelo polinômio 12x³ + 0x² - 4x + 9. Assim teremos:



? R(x) > D(x), podemos dar continuidade à divisão, repetindo o mesmo processo anterior. Achando agora o segundo termo de Q(x).

R(x) < D(x), não damos continuidade a divisão, concluindo que:

O quociente é 6x – 3 e o resto é –19x + 18

Multiplicação de Polinômios

Para efetuar a multiplicação de dois polinômios, multiplicamos cada termo do primeiro polinômio pelos termos do segundo polinômio. Logo apos, somamos os polinômios que tem a parte literal igual.

Exemplo:

A = 2x² +5

B = -5x²y +7x -30 

Assim, temos:

A . B = (2x² +5) . (-5x²y +7x -30)       

A . B = -10x²y +14x³ -60x² -25x²y +35x -150 

*[soma o 10x²y com o 25x²y, repete o resto por nao ter outro monômio com parte literária semelhante.]

A . B = -35x²y +14x³ -60x² +35x -150

Polinômios- Para iniciar

O que são Polinômios? Polinômio é a união de vários monômios. Com a união de monômios temos: Binômio: 3x - 4w = 0 Trinômio: 4x + y - 4z = 0 Polinômio: x + 2y + 3z - 4w = 0 *Monômio é uma expressão algébrica na qual não há operação de adição e/ou subtração entre a parte literal e a parte numérica. Exemplo: 3x = 0 (3x) é um monômio, sendo que (3) é a parte numérica e (x) é a parte literal.

Subtração de Polinômios

Subtraindo 
A= –3x² + 10x – 6 
B= 5x² – 9x – 8. 

B - A= (5x² – 9x – 8) – (–3x² + 10x – 6) → eliminar os parênteses utilizando o jogo de sinal. 

B - A= 5x² – 9x – 8 + 3x² –10x +6 → reduzir os termos semelhantes. 

B - A= 5x² + 3x² – 9x –10x – 8 + 6 

B - A= 8x² – 19x – 2 

Portanto: B - A= (5x² – 9x – 8) – (–3x² + 10x – 6) = 8x² – 19x – 2 

Adição de Polinômios

Adicionando 

A= 4x² – 10x – 5 
B= 6x + 12, 

A+B= (4x² – 10x – 5) + (6x + 12) → eliminar os parênteses utilizando o jogo de sinal. 

A+B= 4x² – 10x – 5 + 6x + 12 → reduzir os termos semelhantes. 

A+B= 4x² – 10x + 6x – 5 + 12 

A+B= 4x² – 4x + 7 

Portanto: A+B= (4x² – 10x – 5) + (6x + 12) = 4x² – 4x + 7